Fingeprintの次元削減によって化合物空間を可視化する

2019年10月26日2021年8月28日

フリーで公開されている化合物データセットを使って、化学構造に基づいて化合物空間（ケミカルスペース）を可視化してみます。

1. 動機
2. 方法
- 2.1. Fingerprintの算出
- 2.2. 次元削減手法
3. 化合物空間を可視化してみる

動機

化合物空間の可視化は、
・データセットに含まれる化合物の中に特異なものがないか
・どのような化合物がどの程度含まれているのか
を把握する上で役立ちます。QSARや機械学習の予測モデルを作成する際にも、データに外挿があるかどうかをざっくりと判断できます。

方法

Fingerprintの算出

それぞれの化合物に対しFingerprintを生成して次元削減することで、平面にplotできるようにします。JohnsonとMaggioraの類似性質原則「類似した化合物は類似した性質を持つ」によれば、似た構造・性質を持つ化合物同士が平面上で近くに分布するはずです。

可視化に使うfingerprintは、MorganフィンガープリントとRDkitフィンガープリントを試してみます。

参照：RDkitで利用可能なfingerprint

次元削減手法

次元削減には、主成分分析（PCA）とUMAPを使ってみます。PCAは最もよく使われますが、データの線形性に基づいて低次元空間に圧縮するため、fingerprintのような0-1データには適さない可能性があります。
それに対して、UMAPは非線形成分を考慮した次元削減手法の一つです。同手法の定番t-SNEのような次元削減を数倍の速さで完了できるため、大きなデータセットにも使えます。

クラスタリングにはkmeans法とSpectralClusteringを使います。
kmeans法は、①クラスタをランダムに設置②近くのデータポイントを加えて重心の位置を更新③更新された重心近くのデータで再度重心を求める、という一連の動作を繰り返すことでクラスタリングします。MoonやSwiss rollなどの非線形データはうまく分類できないことが知られていますが、Spectral Clusteringはそのようなデータにも対応できるそうです。scikit learnのチートシートでもkmeans法でうまくいかない場合の選択肢になっています。

それぞれを組み合わせて、正規分布・線形データを前提とした「PCA × kmeans法」と非線形データ対応の「UMAP × Spectral Clustering 」で、それぞれやってみたいと思います。

ちなみに、化合物の類似度指標としてよく使われる tanimoto係数（2つの化合物間の類似度を0から1で表現。1だと同じ構造）をもとに化合物をクラスタリングする方法もありますが、今回は試していません。

参照：高次元データの次元削減および2次元プロット手法
　　　スペクトラルクラスタリング（SpectralClustering）（クラスタ分析）

化合物空間を可視化してみる

データセットにはMolecule netのLipophilicityを使います。約4200個の化合物について、それぞれのSMILESと実験に基づくlogP（疎水性の指標：オクタノール/水分配係数）が含まれています。

参照：化合物データセット一覧

# packageのimport
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
from sklearn.cluster import SpectralClustering
import umap
from rdkit import Chem
from rdkit.Chem import AllChem
import matplotlib.pyplot as plt
%matplotlib inline

# データセット読み込み
df = pd.read_csv('Lipophilicity.csv')
print(df.info())
df.head(5)

<class 'pandas.core.frame.DataFrame’>
RangeIndex: 4200 entries, 0 to 4199
Data columns (total 3 columns):
CMPD_CHEMBLID 4200 non-null object
exp 4200 non-null float64
smiles 4200 non-null object
dtypes: float64(1), object(2) memory usage: 98.5+ KB None

# MorganフィンガープリントとRDkitフィンガープリントを取得
mols = [Chem.MolFromSmiles(x) for x in df.smiles]
morgan_fps = [AllChem.GetMorganFingerprintAsBitVect(x, 2, 1024) for x in mols]
rdkit_fps = [Chem.RDKFingerprint(x, fpSize=1024) for x in mols]

# fingerprintをDFに格納
df_morgan_fps = pd.DataFrame(np.array(morgan_fps))
df_rdkit_fps = pd.DataFrame(np.array(rdkit_fps))

Morganフィンガープリントは、ある原子から設定した半径（radius）内にある部分構造を数え上げていきます。ECFP（Extended Connectivity Fingerprint）フィンガープリントと似たアルゴリズムで、Morganの半径2はECFP4に相当します。ここでは、radius = 2, 1024 bitのfingerprintを算出します。
RDkitフィンガープリントは原子からの半径ではなく結合長を基準に部分構造を数え上げます。こちらはDaylightフィンガープリントに類似しています。デフォルトでは、最小パス長:1結合 – 最大パス長:7結合まで考慮されます。

得られたfingerprintは、<rdkit.DataStructs.cDataStructs.ExplicitBitVect at xxxxxxxxxxxx>のようなobjectで、そのままでは後続の処理ができないため、データフレームに直します。
　

# kmeansクラスタリング
kmeans = KMeans(n_clusters=8, n_jobs=-1)
kmeans.fit(df_morgan_fps)

# PCAで次元削減
pca = PCA(n_components = 2)
decomp = pca.fit_transform(df_morgan_fps)

x = decomp[:,0]
y = decomp[:,1]

#可視化
plt.figure(figsize=(15,5))

# kmeans法で得られたクラスターで色分け
plt.subplot(1,2,1)
plt.scatter(x, y, c= kmeans.labels_, alpha=0.7)
plt.title("PCA: morgan_fps, cluster")
plt.colorbar()

# logPで色分け
plt.subplot(1,2,2)
plt.scatter(x, y, c= df.exp, alpha=0.7, cmap='spring')
plt.title("PCA: morgan_fps, logP")
plt.colorbar()

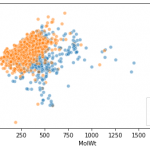
RDkitフィンガープリントで化合物空間を可視化した結果。

同様にdf_morgan_fpsの部分をdf_rdkit_fpsに変えて、RDkitフィンガープリントで可視化してみます。なんとなくRDkitフィンガープリントの方が、キレイに射影されている印象↓

# RDkitフィンガープリントを「UMAP × Spectral Clustering」で可視化
sc = SpectralClustering(n_clusters=50, affinity= 'nearest_neighbors', n_jobs =-1)
sc.fit(df_rdkit_fps)

embedding = umap.UMAP(n_neighbors = 50,
                      n_components = 2,
                      min_dist=0.5).fit_transform(df_rdkit_fps)

x = embedding[:,0]
y = embedding[:,1]

fig = plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
plt.scatter(x, y, c= sc.labels_, alpha=0.7)
plt.title("rdkit_fps, SpectralCluster")
plt.colorbar()

plt.subplot(1,2,2)
plt.scatter(x, y, c= df.exp, alpha=0.7, cmap='spring')
plt.title("rdkit_fps, logP")
plt.colorbar()