目的変数をスケール変換する必要性【機械学習】
機械学習やディープラーニングで、特徴量の変換が重要なことはよく論じられます。例えば以下の書籍など。
一方で目的変数については情報があまりありませんでした。そこで、回帰タスクにおいて目的変数は変換すべきなのかどうか調べた結果をまとめておきます。
目的変数をスケール変換する必要性
当然ですが、場合によってはその必要性があります。
必要となる場面
統計学的には、誤差（残差：実測値と回帰推定値の差）について、以下の2つが成り立たない時とのことです。
・普遍性
・等分散性
最小二乗法で回帰式を求めるとき，前提条件として誤差の不偏性と等分散性があります。誤差の不偏性とは，どんなｘにおいても，誤差の期待値は0となるということです。回帰直線の場合，xのどこでも，平均すれば，誤差は片寄ることなく，その直線上にあることを意味します。
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1182674801
等分散性とは，どんなｘにおいても，誤差のバラツキ（分散）は等しいという意味です。
これらをまとめると，ｘのどこでも，誤差は回帰直線を中心として，その上下に同じようにバラつくことを意味します。ｘのどこでも同じということは，ｘが変化しても，誤差分布はそれに伴って変化しない，つまり無相関であることを意味します。
確認方法
これらは残渣プロット（residual plot）や残渣のQ-Q plotで確認することができます。
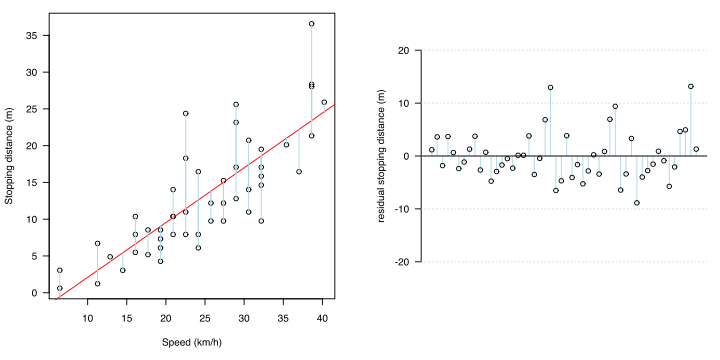
対処方法とスケール変換の種類
つまり、残差を分析して上述の前提条件が成り立たなければ（残渣の在り方になんらかの傾向があるなら）、その回帰モデルは数学的処理により、xとyの関係性をより適切に表現できうると考えられます。その対処法の1つとして目的変数の変換を行います。
例えば、目的変数に指数関数的に大きくなる値をもつとき、予測域が大きい値側になるほど誤差も大きくなります。そのような非線形モデルを線形モデルで表現させるため、対数変換（log）をｙにします。
もっともメジャーなものは対数変換ですが、ほかにも
- √（ルート）変換
- Boxcox変換
- 逆数変換
などがあるようです。
ただし対処法はほかにもあり、変数を増やしたり，２次以上の項を加えたり、評価関数を変更したりするのも考えられます。
目的変数自体が正規分布している必要はない
正規分布している必要があるのは残差なのだ。説明変数や目的変数ではない。これを間違えてはいけない。 残差が正規分布している必要がある理由は、分散分析のF検定の検定統計量の分母に該当するから。F分布は、分母・分子とも正規分布していることが前提だからだ。
回帰分析の説明変数や目的変数は正規分布していなくてもよいか？
回帰分析の評価関数の成り立ちを考えると、正規分布に従わないデータに対しても合うように働くので、ある種もっともな感じです。
以上、目的変数における数値変換の必要性でした。究極的には精度が上がるなら、スケール変換したらいい気がしています。